MH-Net: 论文阅读笔记
MH-Net: 论文阅读笔记
基本信息
论文原文:Revolutionizing Encrypted Traffic Classification with MH-Net: A Multi-View Heterogeneous Graph Model
标题翻译:MH-Net:一种用于加密流量分类的多视角异构图模型
所属会议/期刊:AAAI 2025
一句话总结:一种利用多视角异构流量图进行加密流量分类的模型
背景介绍
- 现有的将深度学习方法用于加密流量分类的问题
现有的基于深度学习的分类方法,在处理流量的粒度上有些僵化,主要体现为:
- 处理单元大小僵化。现有方法通常将一个字节作为最小的处理单元,其实字节可以进一步细分为多个比特。
- 忽视字节间多种关联类型。现有方法将字节序列中不同位置字节的关联混为一谈,无法利用字节在字节序列中的位置差异而带来的信息。
- 核心贡献
提出了MH-Net,一种多视角异构流量图模型:
- 通过将字节拆分成不同比特数目的流量单元,构建多视角图,从而丰富可提取的信息。
- 通过引入基于位置联系的三种类型流量单元对(头-头、头-载荷、载荷-载荷),构建异构图,并采用异构图神经网络提取特征。
- 进一步地,采用多任务对比学习增强流量单元表示的鲁棒性。
方法设计
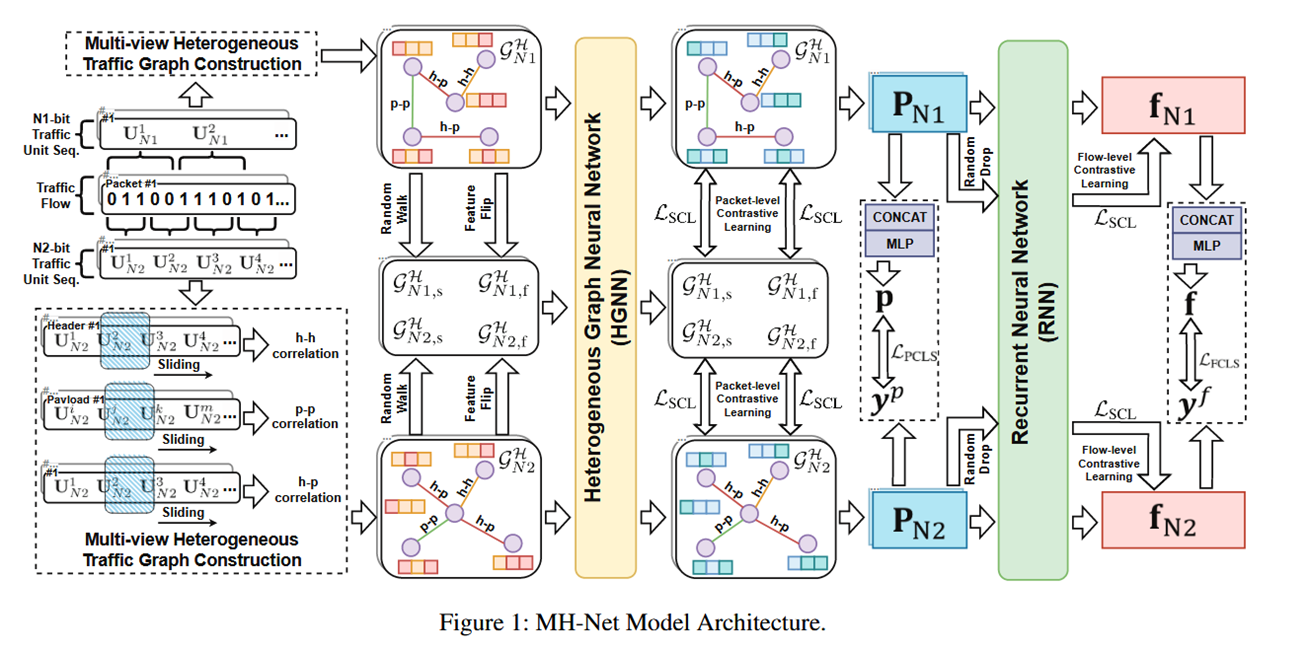
阶段一:构建多视角流量图
- 目的
对一个 数据包(packet) 对应的比特序列,按照不同的流量单元粒度(如4 bits/8 bits)进行划分。在不同比特数量的流量单元能够从不同角度“解释”传输的数据,因此能够挖掘出潜在的、更具判别性的特征。
- 方法
- 将比特序列按照不同比特数,如 $N1$ 、 $N2$ ,作为流量单元,得到两条流量单元序列 $\vec{U_{N1}}$ 和 $\vec{U_{N2}}$。
- 使用
PMI方法量化每一条流量单元序列中,不同流量单元之间的关联性大小。 - 根据第二步的计算结果,将关联性高的流量单元对对应的流量单元结点在图中用边相连。从而得到两张由不同流量单元为结点组成的多视图流量图 $\mathcal{G} _{N1}$ 和 $\mathcal{G} _{N2}$ 。(架构图中未画出这两张图)
- PMI方法
对于流量单元序列 $\vec{U_{N}}$ 来说,第 $i$ 个流量单元序列 $U_{N}^{i}$ 本质就是 $N$ 个比特位,对应一个十进制数。
使用固定大小的滑动窗口扫描流量单元序列,每一个流量单元对应一个数值,统计两个流量单元(即两种数值)在滑动窗口中共同出现的次数,数学表述:
两者同时出现的滑动窗口占总滑动窗口数的占比: $p(U_N^i, U_N^j) = \frac{W(U_N^i, U_N^j)}{W}$
某个流量单元出现的滑动窗口占总滑动窗口数的占比: $p(U_N^i) = \frac{W(U_N^i)}{W}$
PMI值计算: $PMI(U_N^i, U_N^j) = \log{\frac{p(U_N^i, U_N^j)}{p(U_N^i)p(U_N^j)}}$
当PMI值大于0时,被认为两个流量单元具有关联。
阶段二:基于多视角流量图构建其异构图
- 目的
在同一个数据包、不同流量单元构成的两张多视角图 $\mathcal{G} _{N1}$ 和 $\mathcal{G} _{N2}$ 的基础上,对每一张多视角图构建其异构图。这样做是为了能够利用数据包不同位置流量单元之间的联系。
- 做法
流量单元之间的位置关系,具体来说可分为以下三类:
h-h:两个都位于头部的流量单元。p-p:两个都位于载荷部分的流量单元。h-p:一个位于头部、一个位于载荷部分的流量单元。
仍然采用阶段一中的PMI方法,扫描三种序列(头部流量单元序列、载荷部分流量单元序列、完整流量单元序列),从而在图中加入对应类型的边,最终得到图 $\mathcal{G} _{N1}^{H}$ 和图 $\mathcal{G} _{N2}^{H}$ 。
这里的完整流量单元序列,实际上就是阶段一的步骤;所以在实际操作中,阶段一和阶段二可以合成一步,简单来说就是根据PMI方法扫描三条序列,构建图。
阶段三:异构图流量编码器
- 目的
将得到的图 $\mathcal{G} _{N1}^{H}$ 和图 $\mathcal{G} _{N2}^{H}$ 喂给 异构图神经网络(HGNN) ,后者对这些图进行编码,获得可区分的图表示(一个Embedding)。
- 异构图神经网络(HGNN)
异构图神经网络(HGNN)以GraphSAGE作为基本骨干,不同类型的边权重彼此独立不共享。
每一层的前向传播分为两个步骤:采样、聚合,数学表示如下:
在神经网络的第 $l$ 层,在图 $\mathcal{G} _{N}^{H}$ 中的某个节点 v 进行如下计算:
- 邻居节点采样:从邻居节点收集消息,生成消息向量。
$$ m_v^{(l)} = MSG^{(l)}({h_u^{l - 1}, u \in N(v)}; \theta_{h,h}^{l;m},\theta_{p,p}^{l;m},\theta_{h,p}^{l;m}) $$
其中,MSG表示采样函数, $h_v^{l}$ 表示节点 $v$ 在 $l$ 层对应的嵌入向量, $\theta$ 为不同类型边的参数。
- 消息聚合计算:将采样得到的邻居节点信息和自身信息聚合,作为下一层输入。
$$ h_v^{(l)} = AGG^{(l)}(h_v^{(l - 1)}, m_v^{l};\theta_{h,h}^{l;a},\theta_{p,p}^{l;a},\theta_{h,p}^{l;a}) $$
在多层采样-聚合后,最终得到图中的每个节点对应的嵌入向量 $h$,然后逐节点做平均,作为图对应的嵌入向量 $p_N$ ,即包级别特征表示。
$$ p_{N1} = HGNN(\mathcal{G} _{N1}^{\mathcal{H}}) $$
$$ p_{N2} = HGNN(\mathcal{G} _{N2}^{\mathcal{H}}) $$
将一个流中的多个包级别特征表示输入到 循环神经网络(RNN) 中,可以得到相应的对于同一个流的两种流级特征表示,其中 $L$ 为流中的包数目。
$$ f_{N1} = RNN(P_{N1}^1,\dots,P_{N1}^{L}) $$
$$ f_{N2} = RNN(P_{N2}^1,\dots,P_{N2}^{L}) $$
- 模型训练与损失函数
在MH-Net模型进行训练时,其采用的是多任务联合训练的方式,即同时训练包级分类和流级分类,用于进一步优化分类结果。同时,在包级和流级特征生成过程中,采用对比学习。因此,整个系统的损失函数包括四大部分:包级分类损失、流级分类损失、包级对比学习损失、流级对比学习损失。
根据对比学习的损失的反向传播,就会优化模型的能力,从而使得相同label的包/流输出得到的嵌入向量更接近。
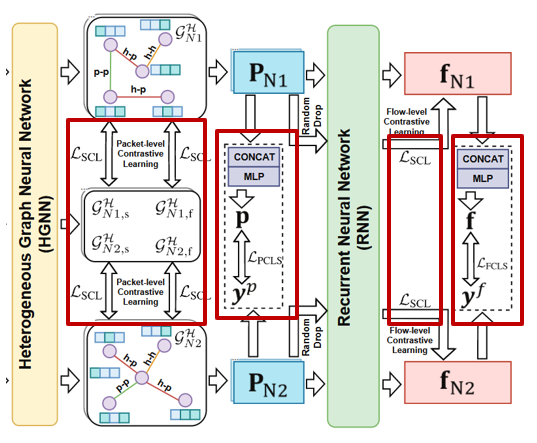
1. 分类损失计算
在得到包/流级特征后,将不同视角的特征值通过CONCAT连接,通过MLP(作者未开源的一个多层流量分类器)预测流量种类,并将其与实际标签做比对,计算得到分类器的损失函数。
包级分类损失:
$$ p = CONCAT(p_{N1}, p_{N2}) $$
$$ \mathcal{L}_{PCLS} = CE(MLP(p), y^p) $$
流级分类损失:
$$ f = CONCAT(f_{N1}, f_{N2}) $$
$$ \mathcal{L}_{FCLS} = CE(MLP(f), y^f) $$
2. 对比学习损失计算
核心损失函数:
$$ \mathcal{L}_{SCL}(z) = \sum _{i \in I}\frac{-1}{| M(i)|} \sum _{m \in M(i)} log \frac{exp(z_i \cdot z_m / \tau)}{ \sum _{k \in K(i)}exp(z_i \cdot z_k / \tau)} $$
这里的 $z$ 指的是来自同一源的两组数据增强的样本组成的嵌入向量集合。
其核心目的在于计算损失后,调节模型的参数,使得正样本之间距离更近,负样本之间距离更远。
包级对比学习损失:
为计算包级别对比学习的损失,需要首先对输入的图进行图增强,将增强后的图也经过HGNN,从而计算对比学习损失。
图增强采用两种方式:1. 随机游走:随机选择一个起始节点出发,生成一个节点序列。提取序列中所有不重复的节点,然后从原图中抽取出由这些节点构成的子图。2. 特征翻转:保持图的结构(节点和边)不变,但是将节点对应的初始字节ID进行了顺序上的翻转。
对于每一张异构图 $\mathcal{G} _{N}^{\mathcal{H}}$ 生成两张增强图 $\mathcal{G} _{N, s}^{\mathcal{H}}$ 和 $\mathcal{G} _{N, f}^{\mathcal{H}}$ 。
包级对比学习损失计算公式为:
$$ \mathcal{L} _{PCL} = \sum _i^{{1,2}}(\mathcal{L} _{SCL}(p _{Ni}, HGNN(g^{\mathcal{H}} _{Ni, s})) + \mathcal{L} _{SCL}(p _{Ni}, HGNN(g^{\mathcal{H}} _{Ni, f}))) $$
总结:一次处理若干个包的嵌入向量(embedding),每个包都包含两个嵌入向量(一个来自原本的图、一个来自增强图)。把所有这些embedding视为总集合,其中每个包的label即为一个类别(增强图的label与原label相同),进行损失计算。
流级对比学习损失:
为计算流级别对比学习的损失,需要获得增强流作为对照。实现的方式是在进入RNN时,丢弃部分包,得到一条增强流的特征。
$$ \mathcal{L} _{FCL} = \sum _i^{1,2} \mathcal{L} _{SCL}(f _{Ni},RNN(p _{Ni}^1 \odot \rho _1,...,p _{Ni}^{Li} \odot \rho _{Li})) $$
总结:一次处理若干条流的嵌入向量,每条流对应两个嵌入向量(原流、增强流),根据流的label划分为不同类型的样本。对于某个具体的嵌入向量来说,与自身对应的流的label相同的嵌入向量为正样本,否则为负样本。
3. 总体损失
根据分类损失和对比损失,可以计算出整个模型的整体损失:
$$ \mathcal{L} = \mathcal{L} _{FCLS} + \mathcal{L} _{PCLS} + \alpha \mathcal{L} _{PCL} + \beta \mathcal{L} _{FCL} $$
其中 $\alpha, \beta \in [0, 1]$ 是用于控制包级别和流级别对比任务的贡献度的参数。
实验分析
实验设置
- 数据集
| 数据集名称 |
|---|
| CIC-IoT |
| ISCX-VPN |
| ISCX-nonVPN |
| ISCX-Tor |
| ISCX-nonTor |
采用的全都是
unb采集的公共数据集。
首先训练并测试流级别流量分类,采取分层抽样的方式,按照9:1划分训练集和测试集。
随后将流的标签扩展至每个数据包的标签,用相应的流的训练集和测试集用来进行包级别流量分类的训练及测试。
- 基线模型
将包级别分类结果和流级别分类结果分别与相应的baseline进行比较,具体包含如下:
包级别基线模型:Securitas,2DCNN,3DCNN,DeepPacket,BLJAN,ESBNN
流级别基线模型:AppScanner,K-FP,CUMUL,ETC-PS,FS-Net,DF,ET-BERT,GraphDApp,TFE-GNN,YaTC
- 评价指标
- 总体准确率 AC
- 宏F1值 Macro F1-score
宏平均值指的是对每一类别分别计算精确率和召回率,然后取算术平均,相当于不管每一类别的样本数量差异,对于最终的宏平均值的贡献度是一样的。适合类别数量相近但样本数差异大的场景,用来强调少数类别表现。
流级别分类任务实验
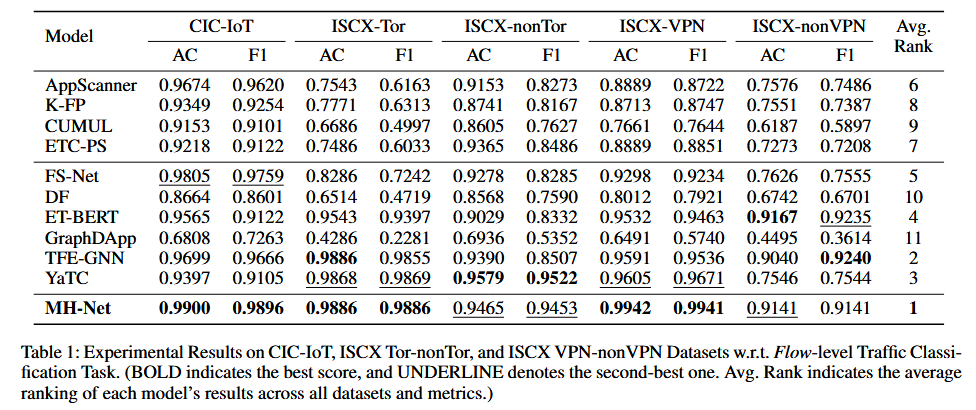
在五个数据集上的平均表现,MH-Net排名首位,随后是TFE-GNN(作者的另一篇论文)和YaTC;
MH-Net的表现远远优于传统的基于统计特征的方法(表格上半部分),相对于基于深度学习方法(表格下半部分),MH-Net仍有明显优势。
TFE-GEN和YaTC也是利用原始字节进行特征表示学习,但仍落后于MH-Net;说明它们对于字节组合利用的不够充分,且忽略了细粒度的字节关联。
在ISCX-nonVPN数据集上,ET-BERT模型的结果十分可观,这是由于其在大规模数据集上利用了大量的参数和预训练,计算负载巨大。
包级别分类任务实验
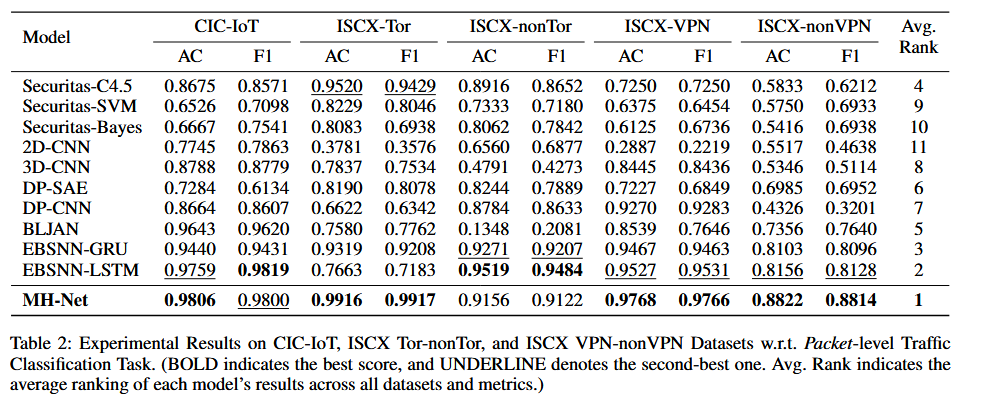
在五个数据集上的平均表现,MH-Net仍然排名首位,随后是EBSNN-LSTM和EBSNN-GRU。
EBSNN在很多数据集上的表现优于MH-Net,但整体仍然和MH-Net有较大差距,说明其能力并不稳定。
消融实验
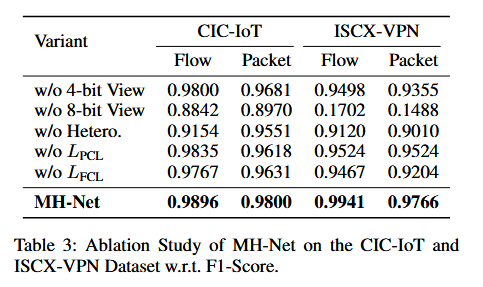
从消融实验可以看出,8-bit的流量单元对于模型分辨流量的贡献度最高,且使用异构图(Hetero.)获取不同位置流量单元间关系的手段是有效的。
参数敏感性分析
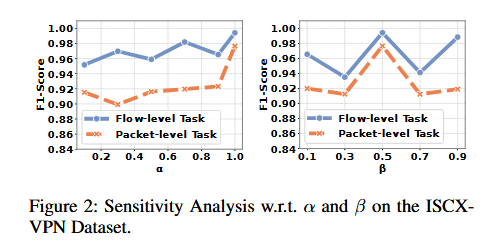
这里的 $\alpha$ 和 $\beta$ 是用来调节整体损失函数中包特征和流特征的对比学习损失占比,可以看出分别取到1.0和0.5的时候,整体效果最好,这也是实验的默认参数设置。
流量单元参数选取
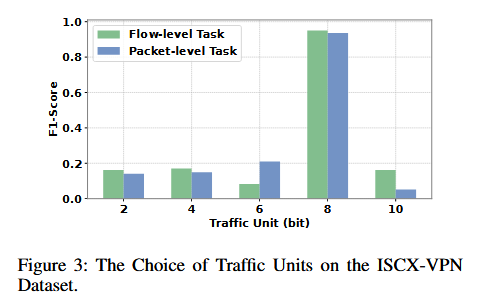
在单一比特量流量单元中,8比特(即1字节)仍然能保持较高的准确率;其他单一比特量流量单元下降的原因可能是破坏了1字节的完整性,而较短的流量单元可能会导致流量图规模增大,降低效率。
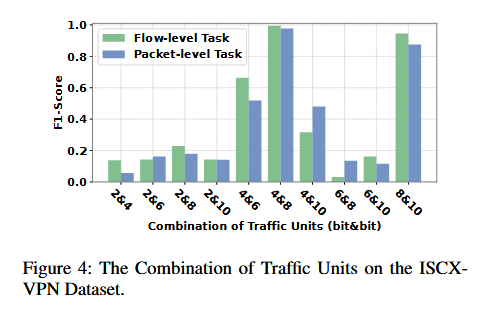
组合不同的流量单元可以一定程度上提升模型性能,实验的默认设置也是选择4比特和8比特的流量单元组合。